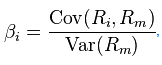by Philip Pilkington
Article of the Week from Fixing the Economists
While doing my dissertation on constructing a new theory of asset-pricing I became exposed to some contemporary theories. To be frank, I didn’t really know how to integrate them because they seemed to be ether (a) intuitively incorrect or (b) useless for what I consider to be the real underlying dynamics of asset-pricing, or (c) some combination of (a) and (b). The CAPM was a combination of both.

It seems to me that the CAPM begs more questions than it answers. Or, at the very least, it restricts the field of inquiry to an extent which I do not think can be properly justified.
The model seeks to estimate a sort of “fair return” on a stock in the stock market. This is represented by what is called the Security Market Line (SML). Any really existing stock that falls above the SML is said to be undervalued (and should thus be bought), while any stock that falls below the SML is said to be overvalued (and should thus not be bought). Here is a graphical representation of the SML.
The point at which that line begins (the intercept), Rf, is the risk-free rate of return. We may think of this, perhaps, as the yield on treasuries or something similar. The Y-axis (vertical) represents the expected return on a given asset, E(Ri), while the X-axis (horizontal) represents the systemic risk or Beta. We will return to this latter component in a moment.
The SML then is the expected return on a well-diversified market portfolio. Thus any assets that are correctly priced will fall along the SML, while any that fall away from it are either over or undervalued.
The questions as regards the non-ergodic axiom begin when we ask what exactly we mean by expected returns, whether these be conceived of as expected returns for the market as a whole, E(Rm), which is represented by the SML, or as expected returns for an individual asset, E(Ri). From what I can tell, most people that use the CAPM derive these values from some sort of fundamental analysis. But the moment we take expectations and other interesting anomalies into account this becomes rather questionable. Although in theory these could be integrated by the analyst into the expected returns but at this point the estimation process becomes a subject of guesswork.
This is where we must come back to our Beta term. The Beta term is the covariance of the return on an individual asset and the market return, divided by the variance of the market return. Or,
To dejargonise that, what it measures is the sensitivity of the individual asset to moves in the market. What is of interest here is that if, say, the entire market moves by X amount what effect will this have on the individual asset.
This, I think, is where the non-ergodic axiom comes into full force. The assumption is that the relationship between moves in the market and in the individual asset are in some way fixed. But one would expect entirely the opposite to be the case.
Take a simple example. Let’s say that we learn that the government of a given country seeks to undertake a stimulus. Now, we know that this will likely boost the stock market of that country because the increased spending will accrue to companies as profits. Added to this, as GDP growth picks up we can be sure that this will boost confidence and so the animal spirits will have their effect too.
Now, let’s say that we want to try to maximise our returns by buying individual stocks in that market rather than just buying into an index fund. We learn from some rather vague announcements that the stimulus will include large outlays for health and infrastructure investment, specifically in the case of the latter, a light rail project. Well, we would then do well by buying up stocks that will be affected by those expenditures most immediately.
I don’t think what I have just said is in any way controversial. Indeed, it seems to me to be simply common sense. But it will mean that the Beta on such stocks will change drastically. Because the relationship between the market and these particular stocks will be differently affected by the coming stimulus we cannot assume that the past values of Beta will hold in the future. So, what will instead? We simply cannot say. But we can make a very intuitive guess and it will be in such a guess that a good deal of profit will be forthcoming.
Such above market profit is usually referred to in the CAPM jargon as “Alpha” and is thought to derive from the stock falling above the SML. But as we have just seen, such “Alpha” may be generated by a change in the underlying Beta due to non-quantifiable but nevertheless comprehensible shifts in the investment flows underlying the market.
Beta, as we have said, seeks to measure systemic risk, but I’m not fully convinced that it does. It also picks up, in a very real way, any changing relation between the overall market and the individual asset. The irony being, of course, that this is precisely what good investors should be interested in. In that very real sense the CAPM hides what is most interesting.
The model gives us a nice story.
“Assuming that the relationship between how the market and the individual asset moves is held constant, here is a representation that will show us whether the individual asset is over or undervalued.”
But it seems to me that often the most interesting and relevant information when picking a stock is to try to figure out where and when this relationship — the Beta — is about to shift and make a bet based on this.
I assume that others, especially those working in markets, will now chastise me.
“Oh, you don’t get it at all. We don’t actually believe that the Beta is fixed or ergodic. We just use this as a rule-of-thumb.”
Such may be the case. But I’m suspicious. I’ve seen too many times before how people using such devices become hypnotised and entranced by them. A clever clogs financier may think that they’re not being fooled by the assumptions of a model but, in my experience, the vast majority of the time the model has the last laugh.